CNT--Classical Nucleation Theory

Posted on Edited on Views:

基本原理

经典成核理论（Classical nucleation theory，CNT）是用于研究成核现象的理论模型。

CNT是建立在成核动力学理论的基础上的，解释了当分子i从气相转移到半径为r的i-mer簇时，系统的吉布斯自由能是如何变化的。这种转变过程被称为气体到粒子的过程。气溶胶形成的吉布斯自由能变化(ΔG)是从蒸汽到团簇的化学势变化，产生团簇表面的自由能，以及溶质分子的溶剂化能的总和，写为

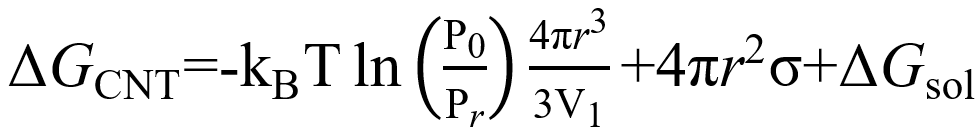
image-20230712111203450

其中kB是玻尔兹曼常数，T是温度，Pr是曲面的蒸气压，P0是周围环境的实际蒸气压，V1是单分子的体积，r是团簇半径，σ是表面张力，ΔGsol是溶质分子的溶解能。

引入相对湿度（RH）和开尔文方程，方程可改写为

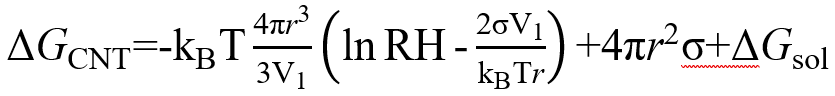
image-20230920144508720

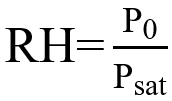
image-20230920144615028

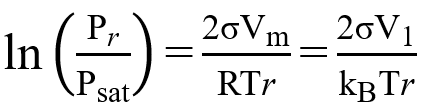
image-20230920144645571

Psat平面的饱和蒸汽压，σ可以从MD模拟得到。

与Molecular Dynamics（MD）结合

接下仅是记录求成核能垒的过程

V1可以利用Multiwfn软件求到：谈谈分子体积的计算 - 思想家公社的门口：量子化学·分子模拟·二次元 (sobereva.com)

RH可以自己设定值，如：0.8、0.9、1.0、1.5等

ΔGsol由Gaussian软件计算得到：谈谈隐式溶剂模型下溶解自由能和体系自由能的计算 - 思想家公社的门口：量子化学·分子模拟·二次元 (sobereva.com)

接下主要说明σ如何求得

首先先计算出团簇得径向数量密度ρ(r)（写代码），使用双曲函数进行拟合（gnuplot），得到液相密度

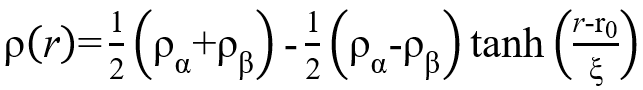
image-20230920150019138

ρα 是液相密度和ρβ是气相密度，气相密度可忽略不计，r为变量，r0为常数值，可以调节函数进行拟合，得到ρα和ξ。

拟合脚本fit.gnu

image-20230920155159475

fit.par

image-20230920155343814

求Irving-Kirkwood压力张量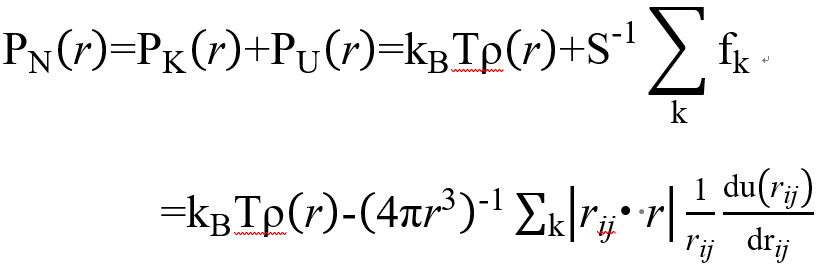image-20230920151617450

fk是作用在表面上的成对分子力的法向分量，u(rij)是分子I和j的成对相互作用能，求导之后就是分子之间的相互作用力，包括范德华和静电（算到每个分子中原子之间的相互作用力，然后投影到质心连线，总的相加就是分子之间的力）

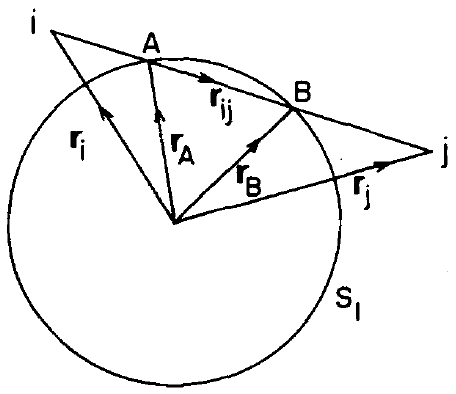
image-20230920152028981

i，j之间可能没有穿过表面、穿过一次表面和穿过两次表面，所以这里需要有一个距离判断，r是某一个表面的半径，需要在rmin和rmax之间才会穿过表面

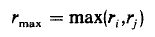
image-20230920152356503

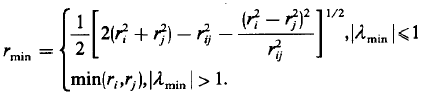
image-20230920152412370

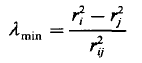
image-20230920152429810

接着还要判断通过λ判断，是一次穿过还是两次穿过，两次穿过的话fk需要乘2

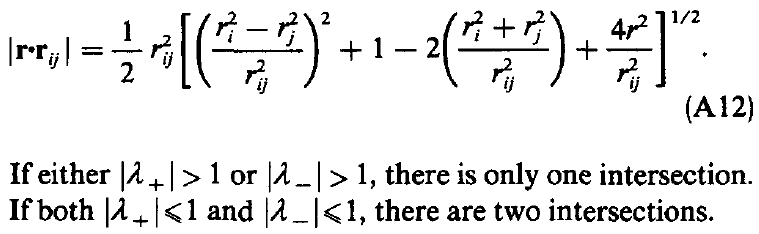
image-20230920152214834

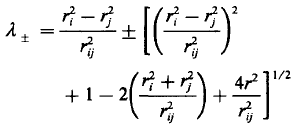
image-20230920154235885

通过对PN(r)的函数进行积分得到W的功

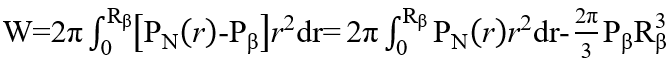
image-20230920154437008

Rβ是球体在蒸汽区的半径，Pβ是蒸汽压。由于蒸气压较低，上述第二项可以省略

接着求团簇的有效半径

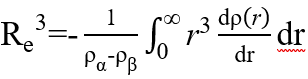
image-20230920150707998

dr之间的数量*r3，然后从0到最大半径处积分

最后通过W和Re得到σ

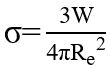
image-20230920154712145

成核速率

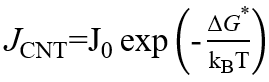
image-20230920154756313

其中J0为指前因子，ΔG*为成核势垒

###因为求Irving-Kirkwood压力张量比较耗时，建议这一步和求ΔG和J分开

参考文献

(1) Farkas, L. Keimbildungsgeschwindigkeit in übersättigten Dämpfen. Z. Phys. Chem. 1927, 125U, 236-242.

(2) Becker, R.; Döring, W. Kinetische Behandlung Der Keimbildung in übersättigten Dämpfen. Ann. Phys. 1935, 416, 719-752.

(3) Frenkel, J. Statistical Theory of Condensation Phenomena. J. Chem. Phys. 1939, 7, 200-201.

(4) Skinner, L. M.; Sambles, J. R. The Kelvin Equation—a Review. J. Aerosol Sci. 1972, 3, 199-210.

(5) Walton, J. P. R. B.; Tildesley, D. J.; Rowlinson, J. S.; Henderson, J. R. The Pressure Tensor at the Planar Surface of a Liquid. Mol. Phys. 1983, 48, 1357-1368.

(6) Li, X.; Hede, T.; Tu, Y.; Leck, C.; Ågren, H. Surface-Active cis-Pinonic Acid in Atmospheric Droplets: A Molecular Dynamics Study. J. Phys. Chem. Lett. 2010, 1, 769-773.

(7) Li, X.; Hede, T.; Tu, Y.; Leck, C.; Ågren, H. Glycine in Aerosol Water Droplets: A Critical Assessment of Köhler Theory by Predicting Surface Tension from Molecular Dynamics Simulations. Atmos. Chem. Phys. 2011, 11, 519-527.

(8) Thompson, S. M.; Gubbins, K. E.; Walton, J. P. R. B.; Chantry, R. A. R.; Rowlinson, J. S. A Molecular Dynamics Study of Liquid Drops. J. Chem. Phys. 1984, 81, 530-542.

(9) Zakharov, V. V.; Brodskaya, E. N.; Laaksonen, A. Surface Tension of Water Droplets: A Molecular Dynamics Study of Model and Size Dependencies. J. Chem. Phys. 1997, 107, 10675-10683.

(10) Vehkamäki, H.; Riipinen, I. Thermodynamics and Kinetics of Atmospheric Aerosol Particle Formation and Growth. Chem. Soc. Rev. 2012, 41, 5160-5173.

(11) Zhao, Z.; Kong, K.; Wang, S.; Zhou, Y.; Cheng, D.; Wang, W.; Zeng, X. C.; Li, H. Understanding Hygroscopic Nucleation of Sulfate Aerosols: Combination of Molecular Dynamics Simulation with Classical Nucleation Theory. J. Phys. Chem. Lett. 2019, 10, 1126-1132.

(12) Zhang, R.; Khalizov, A.; Wang, L.; Hu, M.; Xu, W. Nucleation and Growth of Nanoparticles in the Atmosphere. Chem. Rev. 2012, 112, 1957-2011.

(13) Talanquer, V.; Oxtoby, D. W. Nucleation on a Solid Substrate: A Density Functional Approach. J. Chem. Phys. 1996, 104, 1483-1492.

(14) Liu, L.; Guo, S.; Zhao, Z.; Li, H. Free Energy Prediction of Ion-Induced Nucleation of Aqueous Aerosols. J. Phys. Chem. A 2022, 126, 2407-2416.

(15) Ushcats, M. V.; Bulavin, L. A.; Sysoev, V. M.; Bardik, V. Y.; Alekseev, A. N. Statistical Theory of Condensation – Advances and Challenges. J. Mol. Liq. 2016, 224, 694-712.